https://arxiv.org/abs/1512.03385
Deep Residual Learning for Image Recognition
Deeper neural networks are more difficult to train. We present a residual learning framework to ease the training of networks that are substantially deeper than those used previously. We explicitly reformulate the layers as learning residual functions with
arxiv.org
본 글은 Kaming He가 마이크로소프트에 근무하고 있을 당시 작성한
"Deep Residual Learning for Image Recognition" 논문을 참조합니다.
기본적으로 깊은 뉴럴 네트워크(Deeper neural networks : DNN)는 학습을 진행하면서 필요한 정보들이 점차 줄어들다가 사라지는 기울기 소멸 문제(Vanishing gradient problem) 문제가 발생합니다. ( [딥러닝] 이론(2) - 기울기 소멸 (활성화 함수) 참조 )

위 사진은 각 레이어 (깊이로 나눈) 별로 학습 에러가 얼마나 낮은가를 나타내는 그래프 입니다.
training error와 test error 모두 전체적으로 좋아지는 경향이 있지만,
모델의 깊이가 깊은 56-layer는 비교적 그렇지 않은 20-layer보다 에러율이 더 높게 나타납니다.
즉, 모델의 깊이가 깊으면 깊을수록 성능이 무조건 좋아지는 것은 아닌것 입니다.
이와 같은 상황을 기울기 소멸이라 합니다 모델의 깊이가 깊어질 수록 학습이 진행되지 않는 현상입니다.
해당 문제를 해결하기 위한 방법으로 Kaming He가 제안한 residual learning 방법이 있습니다.
잔차 학습 (residual learning)
잔차 학습이란 일반적인 신경망의 학습 (입력과 출력의 직접적인 매핑) 과 다르게 입력과 출력 간의 차이를 학습하는 방법입니다.
이러한 잔차 학습은 상대적으로 학습이 잘 되기 때문에 모델의 깊이를 더욱 더 깊게 설계할 수 있습니다.
잔차 학습은 정말 간단합니다. 바로 잔여 블록 (Residual Block)을 이용하면 됩니다
Residual Block
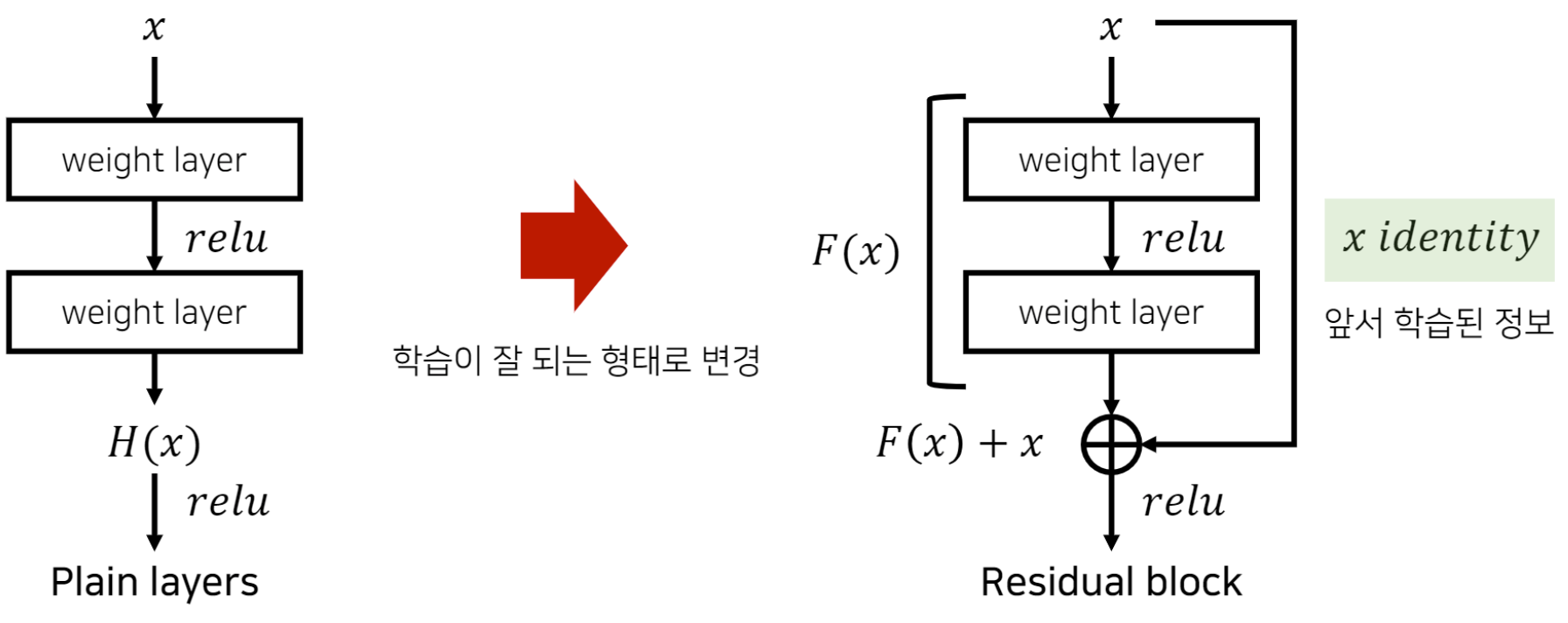
Plain layers
기본적으로 H(x)는 w(weight) x(input) + b(bias) 를 뜻합니다.
입력값에 모든 가중치를 곱하고 바이어스라는 상수값을 더해 가중합이 만들어집니다 그리고 그 가중합에 활성화 함수를 입히면 입력값 x를 출력값 y로 매핑하는 함수 H(x)가 만들어 지는 것이죠.
Residual block
앞서 잔차 학습은 입력과 출력 간의 차이를 학습한다... 라고 했습니다. 그렇다면 이 "차이"란 무엇일까요 바로 F(x)가 그 차이 입니다.
F(x)는 레지듀얼 함수(residual function)라고 하며, 두 개의 합성곱층 사이에 위치합니다.
또한 출력 H(x)과 입력 x에 대한 차 ( F(x) = H(x) - x ) 로 표현할 수 있습니다.
여기서 중요한 점은, 이러한 잔차 F(x)를 0에 가깝도록 혹은 0이 되도록 학습을 진행한다는 것입니다.
만약 F(x)가 0이 된다면, 입력값과 출력이 동일해집니다. 이는 새로운 레이어가 입력값을 변화시키지 않고 그대로 정보를 전달하는 의미가 됩니다. 따라서 입력값을 변화시키는 대신, 레이어를 통과하는 것 만으로도 원하는 출력을 얻을 수 있습니다.
혹시나 "입력과 출력이 같다는 것( F(x)가 0이 됨 )은 학습을 진행하지 못하는 상태 아닌가? " 라고 생각하실 분들을 위해 설명드리겠습니다.
일반적인 딥러닝 모델에서는 각 레이어를 통과할 떄 입력 데이터에 대한 변환을 수행하고, 이러한 변환의 결과는 다음 레이어의 입력으로 전달됩니다.
그러나 떄로는 모델이 특정 입력에 대해 원래의 정보를 유지하는 것이 유용할 수 있습니다(깊은 모델).
잔차 연결은 이러한 목적으로 도입됐습니다. 만약 레이어를 통과하는 입력이 원래의 입력과 출력이 같다면, 이는 해당 레이어가 변환을 하지 않았음을 의미합니다.
이는 신경망이 필요한 경우에만 변환을 수행하고, 그렇지 않으면 입력을 그대로 전달하여 정보를 보존할 수 있음을 뜻합니다.
따라서 잔차 연결의 목표는 입력과 출력이 같아지도록 하는것이 아니라, 입력과 출력이 유사한 경우에는 변환을 거치지 않고 그대로 전달하여 정보를 보존하는 것 입니다.그렇다면 이렇게 잔여 정보를 학습하는게 어떠한 이득이 있을까요?
기존의 Plain layers의 학습 방법을 살펴보시면,
weight layer들이 별도로 분리돼어 있기 때문에 각각의 weight 값을 개별적으로 학습하게 됩니다.
이로 인해 가중치 수렴 난의도가 높아지고, 그 현상은 레이어가 깊어질 수록 문제가 더 심해집니다.
이에 비해 Residual block을 활용한 잔차 학습 방법을 살펴보면
기존의 학습 정보인 x는 그대로 가져오고
추가적으로 필요한 정보 F(x)만 더해주면 됩니다.
따라서 모델의 복잡도와 성능 면에서 큰 발전이 있으며, 모델을 깊게 설계해도 된다 (기울기 손실 극복)는 점이 있습니다.
ResNet (Residual Network)
이러한 잔차 학습 (Residual block)을 활용한 모델이 바로 ResNet 입니다.
ResNet은 층이 총 152개로 구성되어있지만, 레지듀얼 (residual) 학습을 통해 기울기 소멸 문제 없이 학습할 수 있습니다.
VGG19
ResNet은 기본적으로 VGG19 모델의 구조를 뼈대로 합니다.
여기서 VGG 모델이란 Visual Geometry Group의 약자로써 합성곱에 쓰이는 필터(filter)를 3 X 3 크기로 제한해,
모델의 깊이를 깊게 구현한 모델입니다. (필터가 크면 이미지가 급격하게 작아지므로 모델을 깊게 설계하지 못할 뿐더러, 필터 내부의 가중치가 많아져서 더 복잡해지기 때문입니다.)
이러한 모델의 깊이를 19층으로 만든 것이 VGG19 입니다.
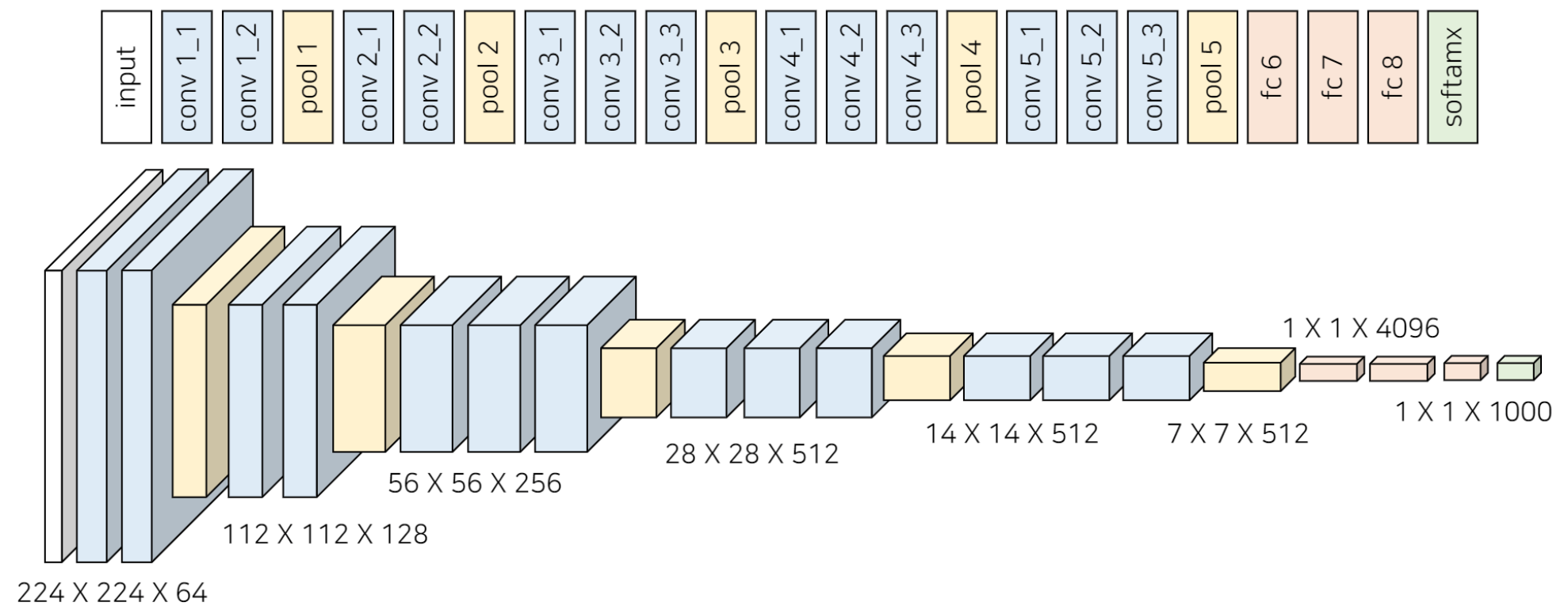
레이어가 깊기 때문에 결과적으로 이처럼 충분히 넓은 영역에서도 고차원적인 특징까지 잘 추출할 수 있게 됩니다. 그러나 이렇게 레이어가 깊다고 무조건 좋은건 아니라고 위에서 계속 강조 드렸습니다.
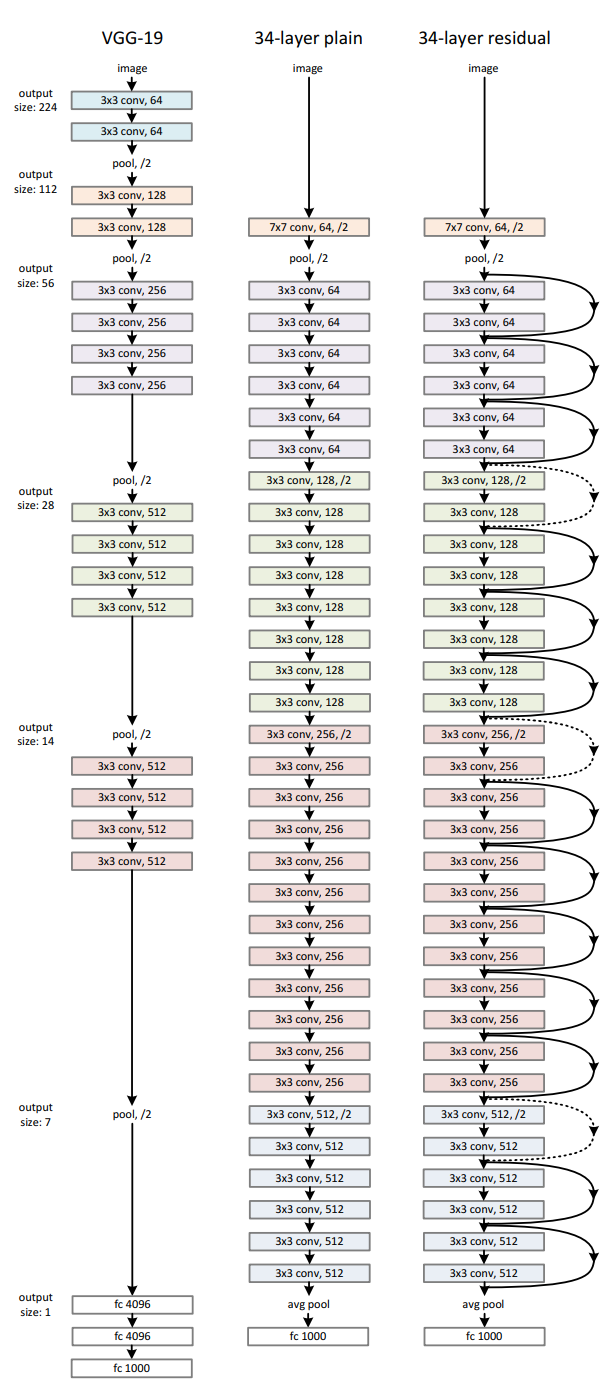
가장 왼쪽 레이어가 VGG19, 가운데가 일반적인 34층 레이어, 오른쪽이 잔차학습을 통한 34층 레이어 입니다.
기본적으로 컨볼루션 필터는 모두 3x3 크기로 이루어져있고, 잔차학습 레이어 같은 경우에는 일반 34층 레이어와 구조가 비슷하지만, 입력값 x를 출력값에 추가시키는 숏컷을 진행합니다.

위 사진은 ResNet의 각 층마다(18, 34, 50, 101, 152)의 summary를 표현한 것입니다.
FLOPs는 딥러닝에서 계산복잡도의 척도입니다.
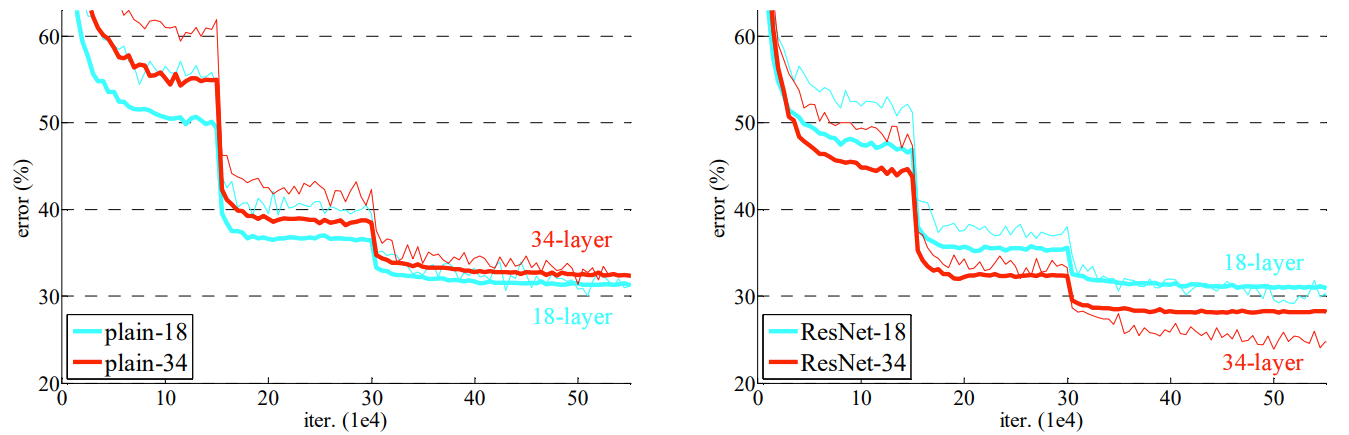
이러한 ResNet은 기존 합성곱신경망에 비해 모델의 깊이가 깊을수록 손실이 적어지는 특징을 보입니다.
'인공지능 > 딥러닝' 카테고리의 다른 글
| [딥러닝] 이론 - 기울기 소멸 (활성화 함수) (0) | 2024.02.03 |
|---|---|
| [딥러닝] 이론 - 과적합 (0) | 2024.01.19 |
| [딥러닝] 이론(2) (0) | 2024.01.19 |
| [딥러닝] 이론(1) (0) | 2023.03.16 |