K-최근접 이웃(K-Nearest Neighbor)은 머신러닝에서 사용되는 분류(Classification) 알고리즘입니다.
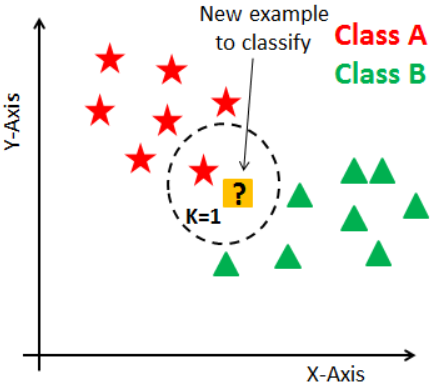
새로운 입력(분류되지 않은 검증 데이터)을 받았을 때 기존 클러스터(군집화)에서 모든 데이터와 인스턴스 기반 거리를 측정한 후 가장 많은 속성을 가진 클러스터에 할당합니다.
실습 - 도미, 빙어 분류
도미와 빙어의 길이(length) 및 무게(weight)를 학습하여 새로운 입력값(length, weight)이 들어왔을 때 도미인지, 빙어인지 분류하는 모델을 만들어보겠습니다.
데이터 생성
# 도미
bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0]
bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, 500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0, 700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0]
# 빙어
smelt_length = [9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
smelt_weight = [6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]도미, 빙어는 각각 길이와 무게의 데이터를 리스트로 가지고 있습니다. 하지만 우리는 한 모델 안에 데이터를 집어넣어야 하므로 이 두개의 데이터를 하나로 합치겠습니다.
데이터 합치기
length = bream_length + smelt_length
weight = bream_weight + smelt_weight
# 2차원 배열로 하나에 생선값을 2개로 만듦
# fish_data_for = [[l,w] for l, w in zip(fish_length, fish_weight)]
import numpy as np
fish_train = np.column_stack((length, weight))
도미 데이터 35개, 빙어 데이터 14개가 fish_train 안에 들어있습니다.
2차원 배열로 되어있는데... 이는 한 물고기 각각 길이와 무게의 데이터를 가지기 때문입니다.
또한 sklearn에서 학습 데이터는 2차원 배열로 돼있어야 합니다.
(column_stack 함수는 두 배열의 각 인덱스 번호에 맞는 데이터끼리 묶어줍니다)
정답 데이터(target) 생성
지도 학습은 정답이 포함된 데이터를 학습시킵니다. 따라서 각 물고기 데이터의 정답을 따로 준비해야합니다.
one = np.ones(35) # 도미
zero = np.zeros(14) # 빙어
# 정답 데이터 통일화
fish_target = np.hstack((one, zero))도미는 1 빙어는 0으로 정답 데이터를 생성했습니다. 예를 들어 (30, 700)인 데이터가 들어오면 출력값은 1이여야 합니다.
fish_target 안에 정답 데이터를 겹쳐 넣은 이유는, 나중에 모델 학습을 할 때 fish_data와 인덱스가 같아야하기 때문입니다.
훈련세트 테스트 세트 나누기 ( train_test_split )
train_test_split 함수는 주어진 데이터를 학습용 데이터와 테스트용 데이터로 나눠줍니다.
인자 값에는 (x, y, shuffle, test_size, random_state)가 있습니다.
왜 이렇게 훈련세트 및 테스트 세트로 나눠야 할까요?
머신러닝 모델을 학습할 때, 전체 데이터를 사용하여 모델을 학습시키면 모델이 전체 데이터에 과적합(overfitting) 됩니다.
쉽게 말해 훈련 데이터로 학습을 시키고 훈련 데이터로 테스트를 시키면 당연히 정확도가 100%가 나옵니다.
따라서 머신러닝 알고리즘의 성능을 제대로 평가하려면 훈련 데이터와 평가에 사용할 데이터가 각각 달라야 합니다.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(fish_data, fish_target, random_state=42)훈련 데이터는 _train에, 평가 데이터는 _test에 저장됐습니다. 이때 'random_state = 42' 를 설정함으로써 데이터셋을 섞을 때 42(설정한 int 값)를 참조하여 섞습니다. 하이퍼파라미터를 튜닝할 때 이 값을 고정해 두어야 매번 데이터셋이 변경되는 것을 방지할 수 있습니다.
데이터 훈련 및 예측
k-최근접이웃 알고리즘으로 모델을 학습시키기 위해서는 sklearn.neighbors의 KNeighborsClassifier 클래스를 사용하여 쉽게 모델을 훈련시킬 수 있습니다.
from sklearn.neighbors import KNeighborsClassifier
# 기본값 5
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_train, y_train)이제 새로운 값을 넣어 도미(1)인지 빙어(0)인지 예측해보겠습니다.
knn.predict([[25,150]])

길이가 25이고 무게가 150인 물고기 데이터를 예측해보았을 때 값은 빙어로 나왔습니다.
하지만 아무리 비교를 해보아도 도미에 더 가깝습니다... 그렇다면 왜 예측값은 빙어로 나오는 걸까요
두 특성(길이, 무게)의 스케일(scale)이 다르기 때문입니다.
길이와 무게는 값의 범위가 매우 다릅니다... 길이는 아무리 길어봤지 40이고 무게는 최대 1000의 범위를 갖고 있습니다.
스케일 조정
스케일 문제를 해결하기 위해서는 표준점수(standard score, z 점수)를 입력 데이터로 사용하면 됩니다.
표준점수는 ' (입력값 - 평균) / 표준편차 '로 구할수 있습니다
또는 sklearn에서 StandardScaler 함수를 사용해 쉽게 구할 수 있습니다.
mean = np.mean(train_input, axis = 0) # axis로 행 기준 처리
std = np.std(train_input, axis = 0)
standard = (train_input - mean) / std # 전처리 된 입력값
knn.fit(standard, train_target) # 재학습
predict_value = ([25, 150] - mean) / std # 예측값
distance, indexes = knn.kneighbors([predict_value])
# 예측값과 가까운 이웃의 거리(distance), 인덱스(indexex)위와 같이 z 점수로 변한 입력 데이터(standard)와 예측 데이터(predict_value)가 준비됐고, 재학습도 시켜줬습니다.
또한 더 정확한 그래프를 그리기 위해 kneighbors() 함수를 사용해 k 거리의 데이터를 알아냈습니다.
plt.scatter(standard[:, 0], standard[:, 1]) # 전체 데이터
plt.scatter(predict_value[0], predict_value[1]) # 예측 값
plt.scatter(standard[indexes, 0], standard[indexes, 1]) # k 거리 데이터
plt.show
'인공지능 > 머신러닝' 카테고리의 다른 글
| [머신러닝] 결정트리 (Decision tree) (0) | 2023.09.22 |
|---|---|
| [머신러닝] 앙상블 학습 (Ensemble Learning) (2) | 2023.08.29 |
| [머신러닝] 전처리 (pre-processing) (1) | 2023.04.11 |
| [머신러닝] 회귀(Regression) 선 그래프 (1) | 2023.04.08 |
| [머신러닝] K - 최근접 이웃 회귀 (K-NN Regression) 01 (0) | 2023.04.08 |